동적계획으로 구현을 위해서는 동적계획 부터 알고 넘어가야겠다. 동적 계획이란...
알고리즘 구현방법 중의 하나로 문제를 해결함에 있어서 기존에 계산된 결과가 있다면 그것을 사용하여 수행 시간을 단축 시키는 방법이다.
그럼 이 동적계획법을 사용하여 TSP를 구현함에 있어서의 기존에 구해진 재귀관계식 부터 살펴보자..맨땅에 헤딩 할 순 없으니깐;;;;;;ㅋ
위의 식을 일반화 해서 i<>1 이고 Vi가 A에 속하지 않을때라 하면 아래와 같이 된다라고 하는....
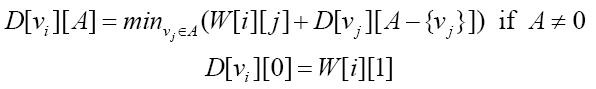
위 수식을 얻는 과정은 알고리즘 책을 봐야겠다...;
.
.
그럼 위의 주어진 재귀식을 통해 프로그램으로 승화 시켜보자~! ㅡ_ㅡ+
일단 필요한 배열들... 동적계획을 위해 계산된 결과를 저장할 이차원 배열 D[][]와 간선들의 가중치를 저장할 배열 W[][]가 있어야겠다. 그럼 여기서 문제되는게 A로 표기된 'V-{vi}' 요녀석을 어떻게 표현 할껀지가 이번 동적계획의 핵심이 되겠다.
검색을 좀 해보게되면 배열(?) 또는 리스트로 담는다는 분들도 있고, bit로 해서 표현한다는 분들도 있는데.. 난 bit로 하기로 결정!
bit로 하게 되었을때 간단히 보면 v1,v2,v3,v4가 있을 때 v1,v2가 포함되어 있다면 0011로 표시될수 있다. 흠 이렇게 하면 이해가 잘 되지 않지만 아래를 보면
|
V4 |
V3 |
V2 |
V1 |
십진수 | |
|
모든 정점이 포함되지 않음 |
0 |
0 |
0 |
0 |
0 |
|
정점 V1이 포함 |
0 |
0 |
0 |
1 |
1 |
|
정점 V2가 포함 |
0 |
0 |
1 |
0 |
2 |
이제 본격적으로 코드를 살표보기로 하자!




